Latente ed esponenziale: come nasce un’epidemia
Un modello computazionale per simulare l'insorgere di un'epidemia e i suoi aspetti anti-intuitivi.
In questo articolo presento un modello computazionale probabilistico multi-agente, da me ideato, con l’intento di aiutare a comprendere l’insorgere di una epidemia, caratterizzato da due comportamenti anti-intuitivi: prima la sua latenza e poi la crescita esponenziale improvvisa.
L’attuale pandemia di Covid-19 ha costretto le popolazioni a confrontarsi con un fenomeno caratterizzato da aspetti di notevole complessità che sono fuori dall'esperienza usuale. Per questo essi rappresentano una notevole sfida per le nostre capacità di comprensione. In particolare mi è parso sia molto difficile la visualizzazione di alcuni concetti chiave coinvolti nelle epidemie. E non “vedere” significa alla fine non capire.
Per questo ho pensato a un semplice modello computazionale interattivo che cerca di simulare l’insorgere di una epidemia generica in una comunità di circa 50.000 persone: quello che potrebbe essere un centro abitato medio-piccolo. Sufficientemente grande per essere significativo ma non troppo per le capacità di calcolo di un comune computer. E non troppo, anche, per poter considerare omogenea la distribuzione di contatti tra gli abitanti, così da poter ignorare l’aspetto spaziale, considerando solo quello temporale, sufficiente, credo, nell'analisi di un focolaio epidemico in una comunità localizzata.
La simulazione
- Qui di seguito si può sperimentare in tempo reale l’esecuzione in sequenza di 6 distinte e indipendenti simulazioni. Questa sessione di simulazioni può essere eseguita in automatico o passo-passo, interrotta, fatta ripartire o annullata tramite i pulsanti sottostanti la parte grafica.
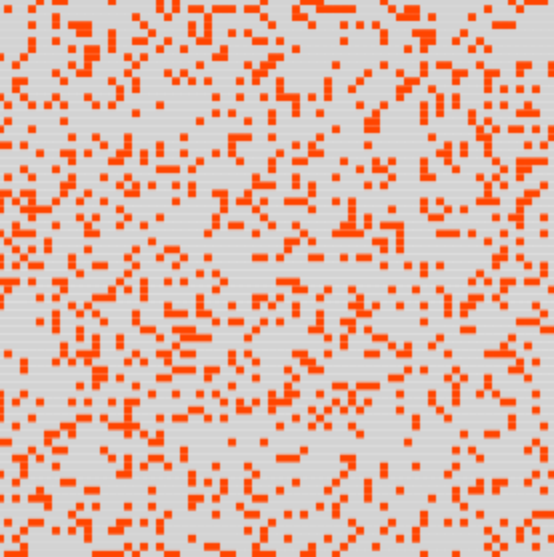
- Ciascuna simulazione prevede un singolo infetto iniziale e può essere osservata nel suo evolvere attraverso una matrice che visualizza lo stato corrente di ciascun membro della popolazione e un grafico che mostra l’ammontare complessivo degli infetti di ciascuna simulazione.
- Ciascuna simulazione si arresta dopo un massimo di 30 passi (cioè “giorni” simulati) o al superamento di 1200 infetti complessivi.
- Ciascuna sessione presenterà un insieme diverso di simulazioni in base alle scelte del generatore di numeri pseudo-casuali presente nel dispositivo utilizzato. Su alcuni di questi potrebbe verificarsi una ripetizione sistematica dello stesso schema. Nel caso provare su un dispositivo di tipo diverso.
- Nonostante sia possibile fruire del modello anche su smart phone è consigliabile utilizzare un computer, per consentire la visualizzazione simultanea di tutta la parte grafica e interattiva su uno schermo grande.
| Simulazione | di totali |
| giorno | Infetti nuovi | Infetti totali |
Avvertenza
Il modello presentato è una descrizione semplificata, anche se credo significativa, di una epidemia generica e non specificatamente di Covid-19. In particolare in queste simulazioni il tempo di raddoppio, nella fase esponenziale, è di circa 2 giorni. Nel caso di Covid-19, invece è, fortunatamente, più alto. Ad esempio in Italia a inizio Marzo 2020 era di circa 3 giorni, mentre a Ottobre 2020 è stato di 7 giorni.
Il Modello
Il modello qui presentato è di tipo multi-agente a tempo discreto e quindi si differenzia dai classici modelli a dati aggregati e tempo continuo basati su equazioni differenziali utilizzati da tempo in epidemiologia (vedi più sotto l’approfondimento sui modelli epidemiologici).
Ho rappresentato ciascun abitante come un elementare oggetto informatico (un “agente”) che può trovarsi in uno di due stati: sano o infetto. Ad ogni passo di simulazione (cioè in ogni “giorno” simulato) per ciascun infetto vengono scelti a caso altri 4 agenti per simulare altrettanti contatti quotidiani. Per ciascuno di questi, se l'agente contattato non è già infetto, l’algoritmo decide di contagiarlo con una probabilità del 10%, incrementando di uno l'insieme degli infetti. Sia la scelta casuale dei contatti che quella del contagio sono realizzate tramite i normali generatori di numeri pseudo-casuali forniti da tutte le piattaforme informatiche.
La scelta di introdurre un elemento probabilistico nel modello lo rende più vicino alla realtà complessa della vita sociale e della trasmissione della malattia e non banalizza il problema che altrimenti sarebbe molto più semplicemente rappresentato da un classico modello a equazioni.
I valori scelti (4 contatti significativi al giorno per ciascun infetto e 10% di probabilità di contagio) mi sono sembrati un ragionevole compromesso tra la realtà e la praticabilità di un tale modello destinato a un pubblico dotato di un normale computer.
La posizione degli agenti nella matrice non ha alcuna importanza, dato che non ho considerato l’aspetto spaziale. Mi sembra utile solo per dare un impatto visivo che spesso i semplici grafici non hanno. Un conto è un numero, un altro è la “visione diretta”, per quanto simulata, della realtà d'interesse.
Il presente lavoro mira alla rappresentazione semplificata del sorgere di un focolaio, quindi il modello considera solo il fenomeno dell'infezione e non le altre fasi epidemiologiche attraversate dai singoli contagiati (incubazione, comparsa dei sintomi, malattia, guarigione, immunità). Nonostante questo il modello è strutturato per essere facilmente estendibile a rappresentare anche questi aspetti e altri più complessi.
Analisi e discussione
Le simulazioni mostrano due distinte fasi di comportamento del sistema. Una prima fase di lento e incerto avvio della durata piuttosto variabile, dominato dal fattore probabilistico. Passata poi una certa soglia, all'incirca di circa 50 infetti, s’innesca una seconda fase del tutto diversa, dove prende il sopravvento una crescita esponenziale e il fenomeno diventa schiettamente deterministico, con il fattore probabilistico che diventa ininfluente. In questa seconda fase l’andamento è lo stesso previsto dai classici modelli a dati aggregati, basati su equazioni differenziali. Inoltre in questa fase il comportamento delle diverse simulazioni è pressoché del tutto identico, diversamente da quello della prima.
Latenza
Un modello multi-agente come quello qui utilizzato sembrerebbe quindi utile solo nel descrivere la prima fase che però è molto importante per capire l’avvio dell’epidemia. E’ una fase silente, di latenza. Il contagio avviene in modo incerto e può richiedere diverso tempo prima che qualche caso grave ne riveli la presenza. Nel frattempo quindi il fenomeno può restare del tutto nascosto. Nella realtà diversi focolai si possono addirittura estinguere da soli perché i pochi contagiati nel frattempo guariscono (aspetto non considerato dal presente modello). Insomma, quando i numeri sono bassi la malattia fatica ad affermarsi, rischiando addirittura di auto-estinguersi. Quando i numeri invece sono alti fermarla è molto difficile, perché prende via via sempre più forza. Non a caso in epidemiologia si usa il termine “focolaio” perché questo è anche il comportamento degli incendi.
Forse un fenomeno di latenza come questo potrebbe spiegare il perché, in un’ottica pandemica, l’esplosione dei casi avviene in alcune particolari luoghi (ad es. regioni o anche nazioni) e solo più tardi in altre, senza che vi sia necessariamente un legame diretto tra di essi. Semplicemente potrebbe essere che diversi focolai emergono, si manifestano in tempi imprevedibili e casuali in luoghi dove già le infezioni sono in realtà presenti e diffuse ma con numeri bassi, in modo latente (uso il termine “latenza” per l’epidemia nel suo insieme e non nel senso in cui talvolta è anche usato, come sinonimo di incubazione, per un singolo individuo, nell'indicare il periodo di tempo immediatamente successivo al contagio).
Il presente lavoro non li prevede, ma considerazioni analoghe varrebbero per singoli, imprevedibili eventi di super-diffusione. Studi recenti hanno evidenziato che la casualità gioca un ruolo importante nell'attuale pandemia. In sintesi pare che solo il 20% dei contagiati sia responsabile dell’80% dei contagi e non solo perché si tratterebbe di persone dalla infettività elevata, ma per la complessità e casualità delle relazioni sociali, oltre che per caratteristiche proprie del virus SARS-Cov-2.
Questo fenomeno è approfondito da un articolo di Zeynep Tufekci, docente all'Università della North Carolina e pubblicato su “The Atlantic” il 30 Settembre scorso (e pubblicato anche, tradotto, nel numero di Internazionale del 30 Ottobre scorso). Ecco un brano:
“Molte persone hanno sentito parlare dell’R0 (erre con zero), il numero di riproduzione di base di un agente patogeno (è il numero medio di infezioni secondarie prodotte da ogni individuo infetto; se un malato infetta in media altre tre persone, l’R0 è 3). Ma a meno che abbiate letto qualche rivista scientifica, è meno probabile che vi siate imbattuti nel fattore K, che misura la dispersione del virus. Il fattore K stabilisce come si diffonde: se in modo costante o in grandi raffiche a causa di persone che ne infettano molte altre in una volta. Dopo nove mesi di raccolta di dati epidemiologici, sappiamo che il SARS-Cov-2 è un agente patogeno sovradisperso, che procede per sovradispersione, ossia tende a creare dei focolai, ma questa nozione non è ancora entrata completamente nel nostro modo di pensare alla pandemia e alle misure di prevenzione.”
(Nota: il fattore K fa riferimento, come R0, a modelli a dati aggregati).
Crescita esponenziale
La seconda fase evidenziata è quella della cosiddetta crescita esponenziale, cioè un fenomeno di aumento molto rapido ben rappresentato matematicamente da una funzione in cui la variabile indipendente, il tempo misurato in giorni nel nostro caso, appare all'esponente di un’espressione di elevamento a potenza. Come esempio semplice si prende di solito la base 2, cosicché si avrebbe la sequenza 2^1, 2^2, 2^3, 2^4, 2^5, … cioè 2, 4, 8, 16, 32, …
Caratteristica tipica dell’esponenziale è la costanza del rapporto tra un valore qualunque e il suo precedente. Tale rapporto costante coincide con la base dell’operazione di elevamento a potenza, nell'esempio appena fatto, quindi, il valore 2, come è facile verificare anche a occhio. Una sequenza di valori di questo tipo è detta anche progressione geometrica, e il rapporto costante appena detto prende il nome di “ragione” della progressione. Un’altro modo equivalente di vedere questa caratteristica, che permette di riconoscere più facilmente una funzione esponenziale, è che il tempo di raddoppio è anch'esso costante. Nella sequenza di base 2 appena vista questo tempo è chiaramente 1, ma varia con il variare della base. Ad esempio, nel caso delle simulazioni del modello proposto sopra, la base vale circa 1,43 e il tempo di raddoppio è di circa 2 giorni.
Un'altra caratteristica tipica della funzione esponenziale è quella di coincidere con la sua variazione o incremento. Cioè la funzione che ogni giorno vale la differenza tra il valore dell'esponenziale di oggi e quello del giorno precedente, è anch'essa un'esponenziale. Lo si può verificare facilmente con la serie in base 2 vista sopra: (4-2), (8-4), (16-8), (32-16), ... vale 2, 4, 8, 16, ... In termini di Analisi Matematica si dice che la funzione esponenziale è uguale alla sua derivata prima e, viceversa, uguale al suo integrale, a meno di un eventuale fattore moltiplicativo costante. Questo è stato di enorme importanza per lo sviluppo della scienza e della tecnica nei secoli passati, perché ha consentito di risolvere molto facilmente le equazioni differenziali delle leggi fisiche in modo analitico o simbolico quando non erano ancora praticabili come oggi i metodi di calcolo numerico che, sebbene già noti, risultavano troppo onerosi senza la rapidità dei moderni calcolatori. Nel caso di un'epidemia, più semplicemente, questa caratteristica implica che se il totale cumulato dei casi ha un andamento esponenziale, lo stesso varrà per i nuovi casi, che ne rappresentano la variazione quotidiana, e viceversa.
Fenomeni e processi naturali che possono essere descritti da tale rappresentazione matematica sono numerosi ma non così frequenti o evidenti da essere familiari al nostro modo di cogliere e pensare la realtà. Spesso, come nel caso delle epidemie, sono fenomeni rari e su scala troppo grande o su tempi troppo lenti perché riusciamo a comprenderli. Alla nostra mente risulta più familiare la crescita lineare, e la sua corrispondente progressione aritmetica, in cui ad essere costante non è il rapporto tra due valori consecutivi, ma la loro differenza (o incremento). Non si tratta tanto di quanto si sia istruiti o esperti, ma della nostra tendenza naturale a pensare in modo “lineare”, cioè proporzionale, e ad aspettarci quindi che se un dato fenomeno è cresciuto da ieri a oggi di una certa quantità, allora farà circa lo stesso da oggi a domani. A peggiorare le cose sta il fatto che anche un fenomeno esponenziale, se non particolarmente rapido, in un arco temporale breve ci appare come lineare e questo rafforza la nostra familiare visione proporzionale delle cose che però in casi come quello delle epidemie diventa illusoria e porta a sottovalutare le conseguenze. Insomma una buona parte della problematicità delle epidemie è dovuta alla loro crescita e propagazione anti-intuitiva che rende tardive le nostre reazioni di contrasto.
Ma per quale motivo un’epidemia ha una dinamica temporale di questo tipo? La ragione di base è comune a tutti i fenomeni di crescita spontanea e risiede nella natura moltiplicativa di tutto ciò che si riproduce in forma identica. Forse la prima formalizzazione, sebbene in altri termini, di un fenomeno simile è dovuta a Leonardo Pisano, detto il Fibonacci, che nel descrivere l’espansione delle popolazioni di conigli formulò nel 1202 la celebre serie numerica che porta il suo nome (serie o successione di Fibonacci: 1, 1, 2, 3, 5 ,8 ,13, 21, 34, 55, ...), molto simile a una progressione geometrica di ragione/base 1,6 e tempo di raddoppio 1,5. Ogni generazione di nuovi conigli si comporta esattamente come quella che l’ha generata, ma moltiplicando il suo effetto, dato che è più numerosa. Considerando il rapporto tra generazioni successive non c'è ragione di credere che cambi al passare del tempo (dato che, come appena detto, il comportamento di ciascuna resta identico). Ma se si conserva costante il rapporto tra ogni nuova generazione e quella precedente, ci troviamo di fronte alla caratteristica tipica, come visto prima, dell’aumento esponenziale. Similmente si comporta un agente patogeno, nel corso di un’epidemia, ad ogni “generazione”: cioè in ogni momento in cui si trasmette e si replica in nuovi soggetti infetti che a loro volta diventano fonte di nuovi contagi.
Nota sui modelli epidemiologici
I classici modelli dinamici a dati aggregati usati in epidemiologia descrivono matematicamente l’evoluzione delle epidemie nel corso del tempo in modo efficace, ma attraverso una rappresentazione aggregata del fenomeno, utilizzando dei valori medi calcolati sulla popolazione coinvolta, vista come un tutt'uno. Questi modelli, a tempo continuo, sono basati su equazioni differenziali che, specie con gli attuali computer, sono facili da calcolare e permettono risultati certi e riproducibili.
E’ il caso dei Modelli a Compartimenti e in particolare del modello SIR, ampiamente utilizzato, con le sue varianti, da quasi un secolo. Costituisce ancora oggi la base di moltissimi studi sulla propagazione delle malattie infettive ed è strumento quotidiano degli studiosi che monitorano la situazione dell’attuale pandemia stimando il suo ormai celebre parametro, il molto citato “numero di riproduzione” Rt (R-zero è semplicemente Rt al tempo zero, cioè all'inizio dell’epidemia).
Parallelamente, negli ultimi trentanni, con l’aumentare delle capacità di calcolo dei computer, hanno preso piede anche altri tipi di modelli, Modelli ad Agenti, basati sulla rappresentazione della popolazione di interesse tramite un gran numero di “agenti” che modellano i singoli individui ed, eventualmente, anche strutture a rete che modellano le interazioni tra di essi.
Questo tipo di rappresentazione, aderente ai paradigmi della pensiero Sistemico e della teoria della Complessità, permette di descrivere aspetti che sfuggono alle analisi basate sui modelli a compartimenti, come ad esempio la diffusione nello spazio delle malattie (e non solo quella nel tempo) e l’emergere di focolai localizzati dovuti a condizioni particolari. Hanno anche trovato impiego anche nelle Scienze Sociali, come l’Economia e la Sociologia e in Ecologia. Per contro sono in genere molto più complessi, sono caratterizzati da un numero maggiore di assunzioni e di parametri, richiedono ingenti risorse di calcolo e sono più difficili da tarare in base ai dati reali osservati.
In ogni caso la simulazione informatica di sistemi complessi, qualunque sia il tipo di modello utilizzato, risulta uno dei più importanti contributi della scienza odierna alle sfide che l’umanità dovrà affrontare nei prossimi decenni. Un concetto che mi pare ben espresso dalle seguenti frasi prese dalla home page di GLEAMviz.org, un sito tecnico dedicato all'argomento.
“Man mano che la popolazione mondiale in crescita diventa più mobile e urbanizzata, i rischi che le epidemie di malattie infettive e le loro minacce associate possano raggiungere proporzioni globali sono in costante aumento. Per limitare efficacemente i danni sociali ed economici causati dalle malattie infettive, gli istituti di salute pubblica devono essere in grado di anticipare l'evoluzione spaziale e temporale delle epidemie e valutare il potenziale impatto delle strategie di contenimento e prevenzione disponibili.”
Note finali
- Il modello computazionale qui presentato è stato scritto in JavaScript ES6, quindi compatibile con la gran parte dei browser aggiornati negli ultimi tre anni. In caso di problemi nel funzionamento delle simulazioni provare ad aggiornare il browser o cambiare il dispositivo utilizzato.
- La parte grafica fa uso della nota libreria JavaScript open-source D3.js (vedi d3js.org).
- Il presente lavoro ha scopo illustrativo ed è pensato per un pubblico non specializzato. Esso riflette le mie personali opinioni e, nonostante abbia avuto cura di produrlo con attenzione e correttezza, non pretende di fornire risultati di comprovato valore scientifico.
- Tutto il contenuto e il codice presente nella pagina è liberamente utilizzabile purché si faccia riferimento all’autore.
- Per eventuali osservazioni e segnalazioni di errori o inesattezze, prego scrivere a contact@alberini.com o lasciare un commento a fondo pagina.
Riferimenti
-
"L’errore matematico (fatale) che non ci fa capire il coronavirus"
Interessante e piacevole articolo sul nostro storico rapporto difficile con l'esponenzialità. -
"Prima gradualmente, poi improvvisamente ..."
Un'efficace e semplice disamina di alcuni concetti anti-intuitivi delle epidemie, nell'ottica della Scienza della Complessità. -
"Prevedere la prossima pandemia" di Alessandro Vespignani, Le Scienze, Marzo 2018 (ripubblicato in Le Scienze Dossier del Settembre 2020)
Un articolo divulgativo completo, ma più impegnativo, sui moderni modelli a rete e multi-agente. -
"Modelli matematici in epidemiologia"
La voce di Wikipedia sui Modelli a Compartimenti in Epidemiologia e il modello SIR, trattati in dettaglio. -
"Modello basato sull'agente"
La voce di Wikipedia sui Modelli ad Agente. -
"This Overlooked Variable Is the Key to the Pandemic. It’s not R"
L'articolo di Zeynep Tufekci sul fattore K che rappresenta la dispersività di una epidemia. -
"GLEAMViz - The Global Epidemic and Mobility Model"
Il sito di modellazione che offre dati e capacità elaborativa per la descrizione visuale e la previsione delle epidemie.
Andrea Alberini, 8 Novembre 2020

Comments powered by Talkyard.